Diagonales de papel:

A lo largo de las clases de la asignatura "Matemáticas y su enseñanza II" hemos seguido explorando más a cerca de los trazos de las figuras geométricas planas, muestra de esto es esta actividad más donde con diagonales de papel del mismo tamaño o con diferente tamaño nos dimos a la tarea de trazar puros cuadriláteros (Figuras de 4 lados), es una manera muy divertida y al mismo tiempo de ponerse a pensar en cuanto a la manera en que acomodas las diagonales de papel, este fue el resultado:

Continuación de las figuras Geométricas

Siguiendo con la entrada anterior me di a la tarea de seguir experimentando diversos trazos con la regla y el compás y estas son otras figuras que realice con el juego de geometría:

Y después utilizando el programa GeoGebra las realice y este fue el resultado:

Explorando las figuras geométricas planas.

Como parte de una actividad en la asignatura de Matemáticas y su enseñanza II se nos encomendó la tarea de trazar figuras utilizando compás, lápiz y regla, para después realizar los mismos trazos en un programa llamado GeoGera, el cual tiene muchas funciones para trabajar este tema en el salón de clases con los niños, ya que permite hacer trazos exactos de las figuras planas, sacar mediatrices, medir los lados, sacar los ángulos de las figuras entre otras muchas funciones , lo cual resulta más entretenido para los niños y ayuda a los niños que tienen un canal de percepción visual. 

Estos fueron los primeros trazos que realice con regla y compás:

Después los realice en GeoGebra:

Estos fueron otros trazos que realice el segundo día:

Después los realice en GeoGebra:

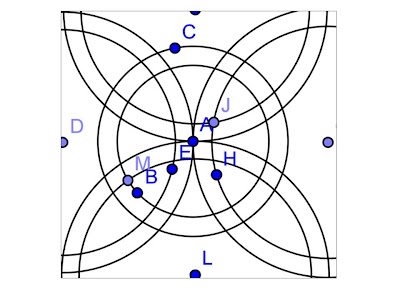
El tercer día use los círculos para trazar estos nudos celtas que encontré en la web, estas figuras representaron el mayor reto de los trazos anteriores usando tanto el compás y la regla como en GeoGebras:

Figuras en GeoGebra:

Publicar entrada

Modelo de Razonamiento de Van Hiele:

Resumen:

En este trabajo les compartiré lo que construí acerca de este tema; Es una teoría de aprendizaje que describe las formas de razonamiento de los estudiantes en la geometría, sus autores son los esposos Pierre y Dina Van Hiele.

Primero que nada se explicara como se da la evolución del razonamiento geométrico en los estudiantes en cuatro niveles que designan los autores, estos niveles traen consigo algunas consideraciones que deben de tener en cuenta los docentes si desean fundamentar sus clases con este modelo. Después nos mencionan los autores una secuencia cíclica para que nosotros como profesores ayudemos a nuestros alumnos a progresar de un nivel a otro, en esta cabe recalcar que las fases son las mismas para cada nivel, lo que las diferencia son los contenidos matemáticos, el lenguaje empleado y la forma de resolver problemas, a pesar de esto como se menciona es un ciclo que se debe seguir su curso en cada nivel para pasar al siguiente.

De manera que este modelo es una orientación para nosotros como futuros docentes en cuanto a nuestras clases que involucren la geometría y podamos estar cada vez mas informados acerca de como es la evolución de los alumnos en esta rama de las matemáticas.

Abstrac:

In this video I will share what I have investigated about this topic; It is a learning theory that describes the forms of reasoning of students in geometry, the authors are husbands Pierre Van Hiele and Dina.

First of all I will explain how happen the evolution of geometric reasoning in students develolpment in four levels that designate the authors, these levels bring some considerations to take into account if teachers want to base their classes on this model. Then, the authors mentioned us a cyclic sequence that we as teachers can use to help our students to progress from one level to another, it is important to emphasize that the phases are the same for each level, the differences are in the mathematical content, language employee and the ways to solve problems, although as mentioned this is a cycle that must take its course in each level in order to get the next one.

So this model that works as a guidance for us as future teachers in our classes that involve geometry and can be increasingly informed about the development of the students in this mathematics branch. 

Mapa conceptual: